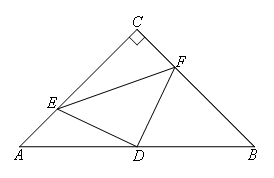
如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化的过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值;其中正确的结论是(    )

①当E，F分别为AC，BC中点时，四边形CEDF是正方形，故选项①正确．
②连接CD，
∵△ABC是等腰直角三角形，
∴∠DCB=∠A=45°，CD=AD=DB；
∵在△ADE和△CDF中，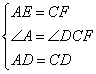

∴△ADE≌△CDF（SAS）；
∴ED=DF，∠CDF=∠EDA；
∵∠ADE+∠EDC=90°，
∴∠EDC+∠CDF=∠EDF=90°，
∴△DFE是等腰直角三角形．故选项②正确．
③∵△ADE≌△CDF，





∴四边形CEDF的面积是定值4，故选项③正确．
①②③均正确，故选D

略