已知:如图,在△ABC中,点D是BC的中点,DF⊥AB,DE⊥AC,垂足分别是F,E,DF=DE,试猜想
AB和AC的数量关系,并证明你的猜想.
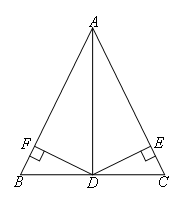
解:AB=AC,理由如下,
∵点D是BC的中点
∴
∵DF⊥AB,DE⊥AC
∴∠BFD=∠AFD=∠AED=∠CED=90°
在Rt△BDF和Rt△CDE中
∴Rt△BDF≌Rt△CDE
∴BF=CE(全等三角形对应边相等)
在Rt△AFD和Rt△AED中
∴Rt△AFD≌Rt△AED
∴AF=AE(全等三角形对应边相等)
∴BF+AF=CE+AE
即AB=AC
请你仔细观察下列序号所代表的内容:
①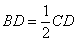 ,②BD=CD,③
,②BD=CD,③ ,④
,④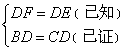 ,⑤SAS,⑥HL,
,⑤SAS,⑥HL,
⑦ ,⑧
,⑧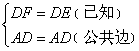 ,以上空缺处依次填写正确的是( )
,以上空缺处依次填写正确的是( )
- A.①③⑤⑧⑥
- B.②④⑥⑧⑥
- C.②④⑥⑦⑤
- D.①③⑤⑦⑤
答案
正确答案:B
略
略








 ,④
,④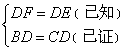 ,⑤SAS,⑥HL,
,⑤SAS,⑥HL, ,⑧
,⑧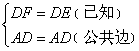 ,以上空缺处依次填写正确的是( )
,以上空缺处依次填写正确的是( )