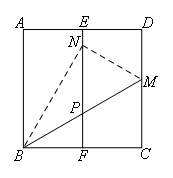
如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论:①CM=DM;②∠ABN=30°;
③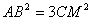;④△PMN是等边三角形.其中正确的有(    )

1．思路分析
本题主要考查折叠的性质以及含30°角的直角三角形三边关系，解决此类问题需要：
①读题标注，梳理信息；本题是正方形背景下的折叠问题，注意折叠是全等变换，折叠前后对应边、对应角相等．据此对相等的边、角进行标注，整理．
②整合条件，合理转化；结合正方形的条件及对应边相等，在直角三角形中根据三边关系可知特殊角度，进而按照选项条件一一验证．
2．解题过程
∵四边形ABCD是正方形
∴BC=CD
∵E，F分别是AD，BC的中点
∴，EF⊥BC
由折叠可知，BN=BC，∠NBM=∠CBM
∴
∴∠BNF=30°，∠NBF=60°
∴∠NBM=∠CBM=30°
∴，
∴
∴，故①错误；
∴，故③正确；
∵EF//AB
∴∠ABN=∠BNF=30°，故②正确．
∵∠BNM=∠C=90°，∠BNF=30°，∠NBM =30°
∴∠PNM=∠NPM=60°
∴△PNM是等边三角形，故④正确．
故选C
3．易错点
不能通过边之间的比例关系，找出对应的角度关系．

略