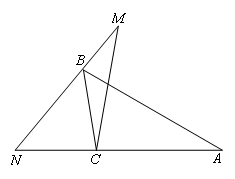
如图,N,C,A三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10.
若△MNC≌△ABC,则∠BCM等于(    )

本题考查全等三角形的性质：全等三角形对应边相等、对应角相等．
1.思路分析：
①分析条件，探索思路：
由∠A：∠ABC：∠ACB=3：5：10，结合三角形内角和定理，可知∠A=30°，∠ABC=50°，∠ACB=100°，要求∠BCM，可以利用∠BCM=∠ACB-∠ACM来求，故只需求∠ACM的度数．
②设计方案，求∠ACM：
由全等三角形的性质，∠ACB=∠MCN，
∴∠ACM=∠ACB-∠BCM=∠MCN-∠BCM=∠BCN，
而∠BCN=180°-100°=80°，
∴∠ACM=80°．
③求解目标：∠BCM=100°-80°=20°，选A．
2.易错点：
①不能利用全等三角形的性质进行角度的转移；
②忽略N，C，A三点在同一直线上，即∠ACN=180°．
3.推荐资源：
若你在全等三角形的性质运用这一块有问题，可以查看视频“2013~2014八年级上册数学预习课人教版，第2课初中数学全等三角形预习课，第1讲全等三角形性质及判定．”
视频链接：http://v.xxt.cn/course/courseview.do?courseId=1349&chapterId=2142

略