如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为点G,连接DG,则图中阴影部分的面积为( )

- A.3
- B.5
- C.
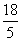
- D.
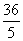
答案
正确答案:C
知识点:勾股定理之折叠问题
1.解答过程:
对于此类求解面积的问题,关键找到对应图形的底和高.此题中阴影部分应以DE为底,过点G往底边AD上做高,求出底和高即可.设出底DE,表达AE,在Rt△AGE中使用勾股定理可求AE,进而求得DE,借助等积公式可算得高,进而求解面积.
2.标准过程:

如图,过点G作GH⊥AD于点H
由折叠,得∠AGE=∠CDE=90°,AG=CD=AB=4,GE=DE
设DE=x,则GE=x,AE=8-x
在Rt△AGE中,由勾股定理,得
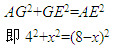
∴x=3
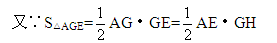
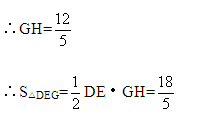
故答案选C.
3.易错点:
答非所问,没有明确目标,考虑问题的思维链条较长,在求出DE或AE长度后忘记本题求解的是面积,易错选A或B;计算三角形面积过程中底乘高除以2,忘记除2,易错选D.
4.视频推荐:
如果此题有问题,建议观看:2013~2014八年级上册数学预习课北师版→初中数学勾股定理预习课→第二讲“勾股定理之折叠问题、等面积法”.
略








