一个等腰三角形的底边长为5cm,一腰上的中线把其周长分成的两部分之差为3cm,则腰长为(    )

（1）考点：等腰三角形的性质
（2）解题过程：
解：如图，在△ABC中，AB=AC，CD为△ABC的中线，BC=5cm

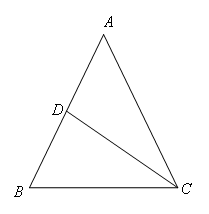
设AD =x，则BD=x，AC=2x
①当（x+2x）-（x+5）=3时，
即2x-5=3
∴x=4
∴2x=8
此时三角形的三边长为8 cm，8 cm，5 cm，满足三角形三边关系，成立
②当（x+5）-（x+2x）=3时，
即5-2x =3
∴x=1
∴2x=2
此时三角形的三边长为2 cm，2 cm，5 cm，不满足三角形三边关系，不成立
综上可得：腰长是8cm．
故选B
（3）易错点：分两种情况讨论是解题的关键：两部分之差可以是底边与腰之差，也可能是腰与底边之差，最后需验证是否能构成三角形.

略