已知二次函数y=ax²+bx+c(a≠0)的图象经过(x₁,0),(2,0)两点,且-2<x₁<-1,图象与y轴正半轴的交点在(0,2)的下方,则下列结论:①abc<0;②b²>4ac;③2a+b+1<0;④2a+c>0.其中正确结论的序号是(    )

根据题干条件可画出二次函数的草图为：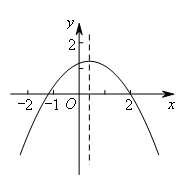
其中a<0，c＞0，根据左同右异可得b＞0，
∴abc<0，故①正确；
∵抛物线与x轴有两个交点，
∴b²-4ac＞0，即b²＞4ac，故②正确；
当x=2时，y=0，即4a+2b+c=0，
∴，
∵0<c<2，
∴2a+b+1＞0，故③错误；
∵二次函数y=ax²+bx+c（a≠0）的图象经过（x₁，0），（2，0）两点，
∴方程ax²+bx+c=0（a≠0）的两根为x₁，2，
∴，即，由x₁<-1得<-1，
∵a<0，
∴c＞-2a，
∴2a+c＞0，故④正确．故选C．

略