已知：如图，A，B为直线l上两点，点为直线l上方一动点，连接，，分别以AC，BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD₁⊥l于点D₁，过点E作EE₁⊥l于点E₁.
（1）如图1，当点E恰好在直线l上时(此时E₁与E重合)，试说明DD₁=AB；
（2）如图2，当D，E两点都在直线l的上方时，试探求三条线段DD₁，EE₁，AB之间的数量关系，并说明理由；
（3）如图3，当点E在直线l的下方时，请直接写出三条线段DD₁，EE₁，AB之间的数量关系.

答案

证明：
(1)如图，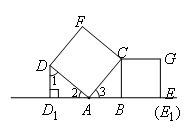

∵DD₁⊥l
∴∠DD₁A=90°
∴∠1+∠2=90°
在正方形ACFD中，
AD=AC，∠DAC=90°
∴∠2+∠3=90°
∴∠1=∠3
在正方形BEGC中，∠CBE=90°
∴∠ABC=90°
∴∠DD₁A=∠ABC=90°
在△DD₁A和△ABC中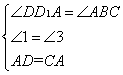

∴△DD₁A≌△ABC(AAS)
∴DD₁₌AB
（2）AB=DD₁+EE₁，理由如下：
如图：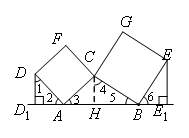

过点C作CH⊥l于点H．
∵DD₁⊥l，EE₁⊥l，EE₁⊥l
∴∠DD₁A=∠AHC=∠CHB=∠BE₁E=90°
∴∠1+∠2=90°，∠4+∠5=90°
在正方形ACFD中：AD=AC，∠DAC=90°
∴∠2+∠3=90°
∴∠1=∠3
在正方形BEGC中：BC=BE，∠CBE=90°
∴∠5+∠6=90°
∴∠4=∠6
在△DD₁A和△AHC中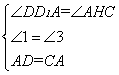

∴△DD₁A≌△AHC（AAS）
∴DD₁=AH
在△CHB和△BE₁E中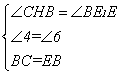

∴△CHB≌△BE₁E（AAS）
∴HB=E₁E
∵AB=AH+HB
∴AB=DD₁+EE₁
(3)AB=DD₁-EE₁．
 

知识点：类比探究  

略

略

下载次数：8

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>