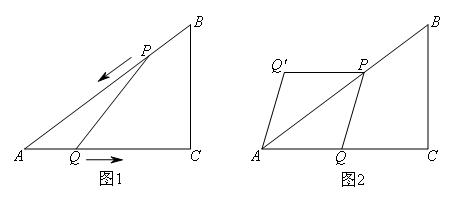
如图1，在△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s，当一个点到达终点时，另一个点也随之停止运动．设运动时间为t（s）．
（1）当t为何值时，PQ∥BC？
（2）是否存在时刻t，使？若存在，求出t的值；若不存在，请说明理由．
（3）如图2，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在时
刻t，使四边形AQPQ′为菱形？若存在，求出t的值；若不存在，请说明理由．

答案

（1）；
（2）t=1或t=4；
（3）.

知识点：相似综合应用——动点背景下的存在性问题  

）（1）由PQ∥BC时的比例线段关系，列方程求解．（2）先表达出△AQP的面积，由列出方程，求解即可．（3）首先根据菱形的性质及相似三角形比例线段关系，求得PQ、QD和PD的长度；然后在Rt△PQD中，求得时间t的值．

略

下载次数：16

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>