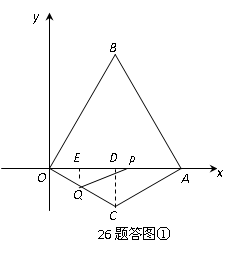
(2010年重庆)已知:如图(1),在平面直角坐标系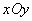 中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P,Q分别从A,O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一点也随之停止.(1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系式,并写出自变量t的取值范围;(2)在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;(3)如图(2),现有∠MCN=60°,其两边分别与OB,AB交于点M,N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M,N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没变化,请求出周长;若发生变化,请说明理由.
中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P,Q分别从A,O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一点也随之停止.(1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系式,并写出自变量t的取值范围;(2)在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;(3)如图(2),现有∠MCN=60°,其两边分别与OB,AB交于点M,N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M,N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没变化,请求出周长;若发生变化,请说明理由.

答案
解:(1)过点C作CD⊥OA于点D.(如图①)∵OC=AC,∠ACO=120°,∴∠AOC=∠OAC=30°.∵OC=AC, CD⊥OA,∴OD=DA=1.在![]() △ODC中,
△ODC中,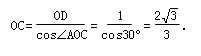 (i)当
(i)当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]() .过点Q作QE⊥OA于点E. (如图①)在
.过点Q作QE⊥OA于点E. (如图①)在![]() △OEQ中,∵∠AOC=30°,∴
△OEQ中,∵∠AOC=30°,∴![]() .∴S△OPQ=
.∴S△OPQ=![]()
![]() .即
.即![]() (ii)当
(ii)当![]() 时,(如图②)
时,(如图②)![]() ,
,![]() ∵∠BOA=60°,∠AOC=30°,∴∠POQ=90°.∴S△OPQ=
∵∠BOA=60°,∠AOC=30°,∴∠POQ=90°.∴S△OPQ=![]()
![]() 即
即![]() .故当
.故当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .(2)D
.(2)D![]() 或
或![]() 或
或![]() 或
或![]() .(3)△BMN的周长不发生变化.延长BA至点F,使AF=OM,连接CF. (如图③)∵∠MOC=60°=∠FAC=90°,OC=AC,∴△MOC≌△FAC.∴MC=CF,∠MCO=∠FCA.∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA=∠OCA-∠MCN=60°.∴∠FCN=∠MCN.又∵MC=CF,CN=CN,∴△MCN≌△FCN.∴MN=NF.∴BM+MN+BN=BM+NF+BN=BO-OM+BA+AF=BA+BO=4.∴△BMN的周长不变,其周长为4
.(3)△BMN的周长不发生变化.延长BA至点F,使AF=OM,连接CF. (如图③)∵∠MOC=60°=∠FAC=90°,OC=AC,∴△MOC≌△FAC.∴MC=CF,∠MCO=∠FCA.∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA=∠OCA-∠MCN=60°.∴∠FCN=∠MCN.又∵MC=CF,CN=CN,∴△MCN≌△FCN.∴MN=NF.∴BM+MN+BN=BM+NF+BN=BO-OM+BA+AF=BA+BO=4.∴△BMN的周长不变,其周长为4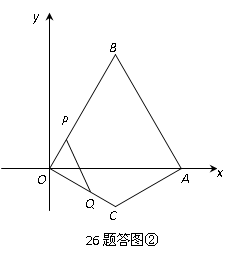 .
.
知识点:运动变化型问题
(1)动点先研究基本图形;(2)研究动点的五个量;(3)表达线段(4)找几何特征(求面积是否能放到直角三角形中、等腰三角形一条线两个圆、周长能否转换)
(1)满足等腰三角形的点D找不全;(2)△BMN的周长找不到问题的突破口









