某科技开发公司研制出一种新型产品，每件产品的成本为2400元，销售单价定为3000元．在该产品的试销期间，为了促销，鼓励商家购买该产品，公司决定商家一次购买该产品不超过10件时，每件按3000元销售；若一次购买该产品超过10件时，每多购买一件，所购买的全部产品的销售单价均降低10元，但销售单价均不低于2600元．
（1）商家一次购买该产品多少件时，销售单价恰为2600元？
（2）设商家一次购买该产品x件，开发公司所获得的利润为y元，求y与x之间的函数关系式，并写出自变量x的取值范围．
（3）开发公司的销售人员发现，当商家一次购买该产品的件数超过某一数量时，会出现随着一次购买数量的增多，公司所获得的利润反而减少这一情况．为使商家一次购买该产品的数量越多，公司所获得的利润越大，公司应将最低销售单价调整为多少元？（其他销售条件不变）
答案
解：（1）50件．
（2）当
时，y=（3000-2400）x=600x
当
时，y= [3000-10（x-10）-2400）]x=
当
时，y=（2600-2400）x=200x
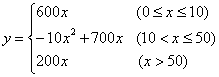
（3）一次函数y=600x与y=200x均为y随x增大而增大，二次函数
，
当
时，y随x增大而增大；
当
时，y随x增大而减小；
因此，当x=35时，销售单价最低，最低单价为3000-10（35-10）=2750元．
知识点：函数类应用题
略
略
WORD格式（
