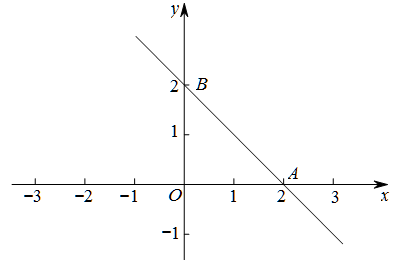在平面直角坐标系中,直线y=-x+m经过点A(2,0),交y轴于点B,点D为x轴上一点,且S△ABD=1.
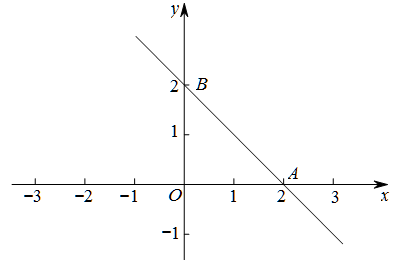
(1)求m的值;(2)求线段OD的长;(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
答案
解:(1)∵直线y=-x+m经过点A(2,0),
∴0=-2+m,
∴m=2;
(2)∵直线y=-x+2交y轴于点B,
∴点B的坐标为(0,2),
∴OB=2,
∵![]() ,
,
∴AD=1,
∵点A的坐标为(2,0),
∴点D的坐标为(1,0)或(3,0),
∴OD=1或OD=3;
(3)①当点D的坐标为(1,0)时,如图所示,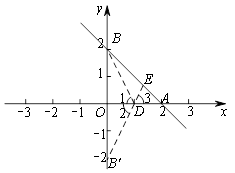
取点B′(0,-2),连接B′D并延长,交直线BA于点E.
∵OB=OB′,AO⊥BB′于点O,
∴OD为BB′的垂直平分线.
∴DB=DB′,
∴∠1=∠2.
又∵∠2=∠3,
∴∠1=∠3,设直线B′D的解析式为y=kx-2(k≠0),
∵直线B′D经过点D(1,0),
∴0=k-2,
∴k=2,
∴直线B′D的解析式为y=2x-2,联立得![]() ,解得
,解得![]() ,
,
∴点E的坐标为![]() ;
;
②当点D的坐标为(3,0)时,如图所示,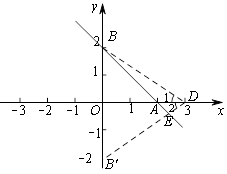
取点B′(0,-2),连接B′D,交直线BA于点E,同①的方法,可得∠1=∠2,
直线B′D的解析式为![]() ,
,
联立得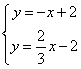 ,
,
解得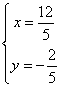 ,
,
∴点E的坐标为![]() ,
,
综上所述,点E的坐标为![]() 或
或![]() .
.
略
略