在平面直角坐标系中，二次函数的图象与x轴交于A（-3，0），B（1，0）两点，与y轴交于点C．
（1）求这个二次函数的解析式；
（2）点M为抛物线上一动点，在x轴上是否存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由．

答案

解：（1）将A（-3，0），B（1，0）代入，可得：
（2）存在；
理由：①当AC为平行四边形的边时：
MQ∥AC
若M在x轴上方，则MC∥QA，MC=QA
由C（0，2）可知点M的纵坐标为2，
代入抛物线解析式得M₁（-2，2）
∴QA=MC=2
由A（-3，0）知Q₁（-5，0）
若M在x轴下方，则四边形MACQ为平行四边形，
则C与M到x轴的距离相等，
由C（0，2）知M的纵坐标为-2，
代入抛物线解析式得M₂（，-2），M₃（，-2）
∴Q₂（，0），Q₃（，0）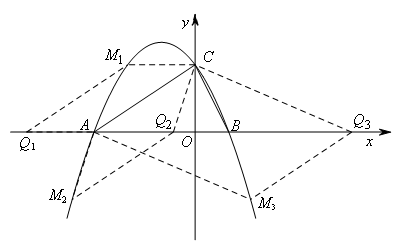

②当AC为平行四边形的对角线时，MQ过AC的中点（，1）
∴M在x轴上方，∴MC∥AQ
∴M（-2，2）
由MQ中点（，1）可得Q₄（-1，0）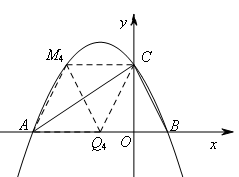

综上所述：Q₁（-5，0）；Q₂（，0）；Q₃（，0）；Q₄（-1，0）

知识点：二次函数综合题  

略

略

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>