如图，在平面直角坐标系中，O为坐标原点，Rt△OAB的直角边OA在x轴的正半轴上，点B坐标为（，1），以OB所在直线为对称轴将△OAB作轴对称变换得△OCB．现有动点P从点O出发，沿线段OA向点A运动，动点Q从点C出发，沿线段CO向点O运动，两点同时出发，速度都为每秒1个单位长度．设运动时间为t秒．

（1）求∠AOC的度数；
（2）若四边形BCQP的面积为S（平方单位），求S与t之间的函数关系式；
（3）设PQ与OB交于点M，当△OMQ为等腰三角形时，求t的值．

答案

解：（1）∵在Rt△OAB中，AB=1，OA=，
∴在Rt△OAB中，由勾股定理得，OB=2
∴∠BOA=30°由轴对称性质，∠COB=30°
∴∠AOC=60°
（2）过Q作QE⊥x轴于E由轴对称性质，△COB≌△AOB
∴=2×××1=
∵OP=t，CQ=t在Rt△QEO中，∠AOC=60°
∴QE=
∴=
∵=
∴=--=（）
（3）
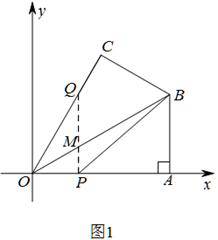
（i）如图1所示，若OM=MQ，∠MQO=∠QOM=30°，
∵∠AOC=60°，
∴∠OPQ=90°，
∴OP=OQ，即t=，
解得t=
（ii）
如图2所示，若OM=OQ，∠OMQ=∠OQM=75°，
∵∠AOC=60°，
∴∠OPQ=45°，
过点Q作QF⊥OA，垂足为F，
则有：FQ=FP，即
解得：t=1．
（iii）若MQ=OQ，∠OMQ=∠QOM=∠POM，则QM∥OA，显然不满足题意．

知识点：一次函数动点问题  

略

略

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>