如图，在平面直角坐标系中，直线y＝x＋1与y＝-
x＋3交于点A，两直线分别交x轴于点B和点C，点D是直线AC上的一个动点．
（1）求出点A，B，C的坐标；
（2）在直线AB上是否存在点E，使得以点E，D，O，A为顶点的四边形是平行四边形？如果存在，求出点E的坐标；如果不存在，请说明理由．
答案
解：（1）∵点B是直线y＝x＋1与x轴的交点
∴点B的坐标为（-1，0）
∵点C是直线y＝-
x＋3与x轴的交点
∴点C的坐标为（4，0）
∵点A为直线y＝x＋1与直线y＝
的交点
联立：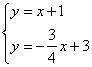
解得：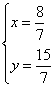
∴点
的坐标为（
）
（2）
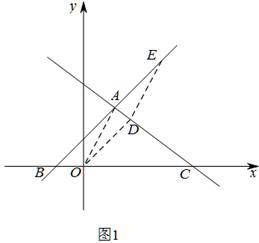
如图1，当四边形OAED为平行四边形时
∵AB∥OD
∴直线OD解析式为：y＝x
∵点D为直线OD与直线AC的交点
联立：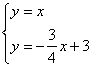
解得：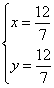
∴D（
）
∵A（）
∴E（
）
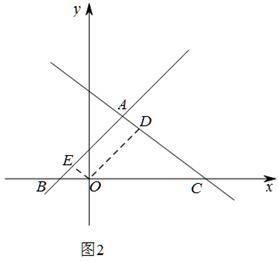
如图2，当四边形ODAE为平行四边形时
∵OE∥AC∴直线OE的解析式为：y＝
x
∵点E为直线OE与直线AB的交点
联立：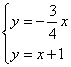
解得：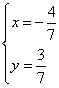
∴E（
）
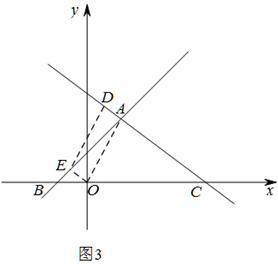
如图3，当四边形OADE为平行四边形时
∵OE∥AC
∴直线OE的解析式为：y＝x
∵点E为直线OE与直线AB的交点
联立：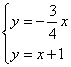
解得：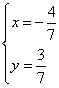
∴E（）
综上可得：E的坐标为（）或（）
知识点：一次函数存在性
略
略
WORD格式（
