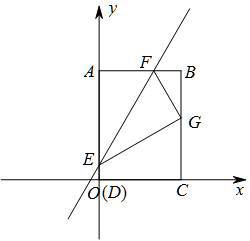
如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,E,F分别在AD,AB上,且F点的坐标是(2,4).
(1)求G点坐标;
(2)求直线EF解析式;
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
答案
解:(1)∵F(2,4),B(3,4),四边形ABCD是矩形
∴AF=2,OA=BC=4,AB=3
在Rt△BFG中,
由轴对称性质
FG=AF=2
∵BF=AB-AF=1
∴BG=![]()
∴G(3,4-![]() )
)
(2)设y=kx+b
∵在Rt△BFG中,
BF=![]() FG
FG
∴∠BGF=30°
∴∠AFE=∠EFG=60°
在Rt△AEF中,AF=2
∴AE=![]()
∴E(0,4-![]() )
)
∴b=4-![]()
∵|k|=![]() =
=![]()
∴y=![]() x+4-
x+4-![]()
(3)存在.
①M(![]() ,
,![]() )
)
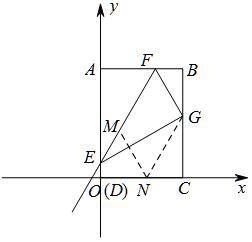
提示:如图,过G作EF的平行线交x轴于点N,过N作FG的平行线交EF于点M,连接MN,GN.则四边形MNGF为平行四边形.利用特殊角及平行四边形性质求点M坐标即可.
②M(![]() ,
,)

提示:如图,MN∥FG且MN=FG,所以四边形MNFG为平行四边形.此时△NHM是边长为2的等边三角形.
③M(![]() ,
,![]() )
)
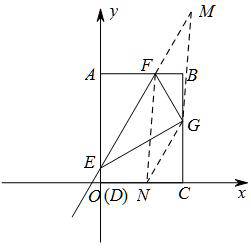
提示:如图,过G作EF的平行线交x轴于点N,连接NF,过G作NF的平行线交直线EF于点M,连接GM.则四边形MFNG是平行四边形.
知识点:一次函数与几何综合
略
略








