已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA,NB分别相交于点D,E.(1)如图1所示,当直线l与直线MA垂直时,猜想线段AD,BE,AB之间的数量关系,写出结论并证明;(2)如图2所示,当直线l与直线MA不垂直且交点D,E都在AB的同侧时,(1)中的结论是否成立?如果成立,请证明:如果不成立,请说明理由;(3)如图3所示,当直线l与直线MA不垂直且交点D,E在AB的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段AD,BE,AB之间还存在某种数量关系吗?如果存在,请写出它们之间的数量关系.
答案
解(1)AB=AD+BE
证明:延长AC交BN于点F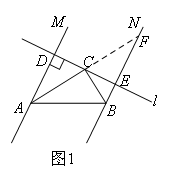
∵AC、BC分别是∠MAB、∠NBA的平分线
∴∠DAC=∠BAC,∠ABC=∠EBC
∵MA∥NB
∴∠DAC=∠BFC
∴∠BAC=∠BFC
∴△ABF是等腰三角形
∴AB=BF,AC=CF
∵∠ACD=∠FCE
∴△ACD≌△FCE
∴AD=EF
∴AB=BF=BE+EF=BE+AD
(2)成立理由:延长AC交BN于点F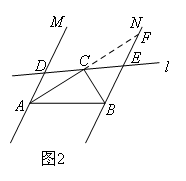
∵AC、BC分别是∠MAB、∠NBA的平分线
∴∠DAC=∠BAC,∠ABC=∠EBC
∵MA∥NB
∴∠DAC=∠BFC
∴∠BAC=∠BFC
∴△ABF是等腰三角形
∴AB=BF,AC=CF
∵∠ACD=∠FCE
∴△ACD≌△FCE
∴AD=EF
∴AB=BF=BE+EF=BE+AD
(3)不成立,存在另外的数量关系.
分两种情况:如图3①:BE=AB+AD;如图3②:AD=AB+BE.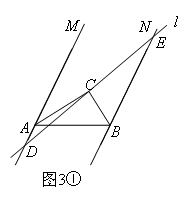
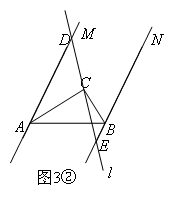
知识点:四边形中的类比探究
略
略








