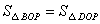如图，A、B分别是x轴上位于原点左、右两侧的点，点P(2，p)在第一象限，直线PA交y轴于点C(0，2)，直线PB交y轴于点D，．（1）△COP的面积是多少？（2）求点A的坐标及p的值.（3）若，求直线BD的函数解析式.

答案

解：（1）如图，过点P作PF垂直于y轴，垂足为F．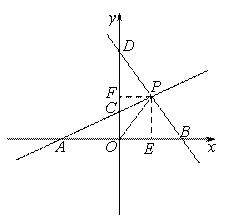

由题意可得PF=2，CO=2，
∴S_△COP=
（2）∵S_△AOP=S_△AOC+S_△COP，即6=S_△AOC+2，
∴S_△AOC=4，即∴AO=4，即点A（-4，0）
设AC所在直线的表达式为y=kx+b（k≠0），分别把A（-4，0）、C（0，2）代入表达式可求得：
，即
把P（2，p）代入，解得p=3
（3）如上图，过P做PE垂直于x轴，垂足为E
∵
∴S_△BOD=2S_△BOP即
∴DO=2PE=6，即点D（0，6）
又由直线BD过点P（2，3）、D（0，6），
代入可得直线BD的表达式为．

知识点：求解一次函数表达式  

略

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>