（2011东营）在平面直角坐标系中，现将一块等腰直角三角板ABC放在第一象限，斜靠在两坐标轴上，且点A(0，2)．点C(1，0)，如图所示；抛物线经过点B．（1）求点B的坐标；（2）求抛物线的解析式；（3）在抛物线上是否还存在点P(点B除外)．使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在．请说明理由．

答案

解：（1）过点B作BD⊥x轴于点D,
∵∠BCD+∠ACO=90°，∠ACO+∠OAC=90°，
∴∠BCD=∠AOC；
又∵∠BDC=∠COA=90°，BC=CA,
∴△BCD≌△CAO,
∴BD=OC=1，CD=AO=2，
∴B点为（3,1）．
（2）将点B（3,1）代入抛物线中，得：9a-3a-2=1，解得：a=，
∴抛物线解析式为：．
（3）假设存在点P，使得△ACP是直角三角形：
①若以AC为直角边，点C为直角顶点．延长BC至点P₁，使得CP₁=BC，得到等腰直角三角形ACP₁．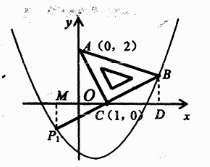

过点P₁作P₁M⊥x轴于点M．
∵CP₁=BC，∠MCP₁=∠BCD，∠CM P₁=∠CDB=90°，
∴△M P₁C≌△DBC，
∴CM=CD=2，P₁M=BD=1
∴P₁点为（-1，-1）经验证，点P₁（-1，-1）在抛物线上，因此P₁满足条件．
假设存在点P，使得△ACP是直角三角形：①若以AC为直角边，点A为直角顶点．
过点A作AP2⊥AC，且AP₂=AC，得到等腰直角三角形ACP₂．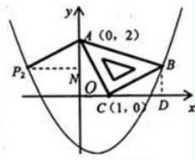

过点P₂作P₂N⊥y轴于点N．
∵∠P₂AN+∠OAC=90°，∠OAC=∠OCA=90°，
∴∠P₂AN=∠OCA
又∵AP₂=AC，∠AN P₂=∠COA=90°，
∴△A P₂N≌△CAO，
∴AN=CO=1，P₂N=AO=2
∴P₂点为（-2，1）．经验证，点P₂（-2，1）在抛物线上，因此P₂满足条件．
②若以AC为直角边，点A为直角顶点．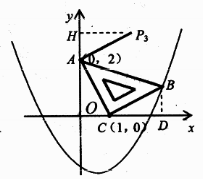

过点A作AP₃⊥AC，且AP₃=AC，得到等腰直角三角形ACP₃．
过点P₃作P₃H⊥y轴于点H．
∵∠P₃AH+∠OAC=90°，∠OAC=∠OCA=90°，
∴∠P₃AH=∠OCA
又∵AP₃=AC，∠AHP₃=∠COA=90°，
∴△A P₃H≌△CAO，
∴AH=CO=1，P₃H=AO=2
∴P₃点为（2，3）．经验证，点P₃（2，3）不在抛物线上．
综上所述，满足条件的P点坐标有P₁（-1，-1），P₂（-2，1）．

知识点：二次函数综合题  

略

略

下载次数：6

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>