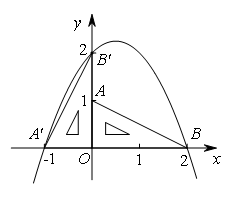
（2012山东菏泽）如图，在平面直角坐标系中放置一直角三角板，其顶点为A（0，1），B（2，0），O（0，0），将此三角板绕原点O逆时针旋转90°，得到△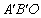
.（1）一抛物线经过点
、
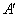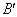、B,求该抛物线的解析式；（2）设点P是在第一象限内抛物线上的一动点，是否存在点P，使四边形
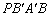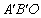的面积是△面积的4倍？若存在，请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，试指出四边形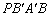是哪种形状的四边形？并写出它的两条性质.
.（1）一抛物线经过点
、
、B,求该抛物线的解析式；（2）设点P是在第一象限内抛物线上的一动点，是否存在点P，使四边形
的面积是△
答案
解：（1）△A′B′O是由△ABO绕原点O逆时针旋转90°得到的，又A（0，1），B（2，0），O（0，0），
∴A′（-1，0），B′（0，2）．
设抛物线的解析式为：y=ax2+bx+c（a≠0），
∵抛物线经过点A′、B′、B，
∴
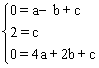，解得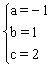
，
∴满足条件的抛物线的解析式为y=-x2+x+2．
（2）∵P为第一象限内抛物线上的一动点，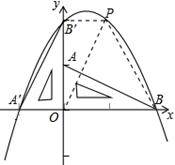
设P（x，y），则x＞0，y＞0，P点坐标满足y=-x2+x+2．
连接PB，PO，PB′，
∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB，
=
×1×2+×2×x+×2×y，
=x+（-x2+x+2）+1，
=-x2+2x+3．
假设四边形PB′A′B的面积是△A′B′O面积的4倍，
则-x2+2x+3=4，
即x2-2x+1=0，解得：x=1，
此时y=-1+1+2=2，即P（1，2）．
∴存在点P（1，2），使四边形PB′A′B的面积是△A′B′O面积的4倍．
（3）四边形PB′A′B为等腰梯形，答案不唯一，下面性质中的任意2个均可．
①等腰梯形同一底上的两个内角相等；②等腰梯形对角线相等；③等腰梯形上底与下底平行；④等腰梯形两腰相等．
或用符号表示：①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′；②PA′=B′B；③B′P∥A′B；④B′A′=PB．
知识点：中考压轴之函数类问题
略
略
WORD格式（
