如图,菱形ABCD中,点M、N分别是BC,CD上的点,且∠B=∠MAN=60°,若∠BAM=20°,求∠CMN的度数.
答案
证明:如图,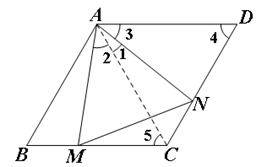
在菱形ABCD中,AB=BC=C D=AD,∠B=∠D
∵∠B=60°
∴∠D=60°
∴△ACD是等边三角形
同理,△ABC是等边三角形
∴AC=AD,∠CAD=60°,∠5=60°
∴∠1+∠3=60°
∵∠MAN=60°
∴∠1+∠2=60°
∴∠2=∠3
而∠5=∠4
∴△ACM≌△ADN
∴AM=AN
∴△ANM是等边三角形
∴∠AMN=60°
∵在△ABM中,∠B=60°,∠BAM=20°
∴∠BMA=100°
∵∠BMA+∠AMN+∠CMN=180°
∴∠CMN=180°-(∠BMA+∠AMN)=180°-(100°+60°)=20°
即∠CMN=20°
知识点:菱形大角夹半角
略
略








