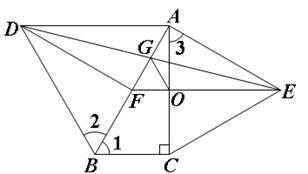
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG.其中正确结论的序号是(),并说明理由.
答案
解:①③④理由如下:
如图
在等边△ABD中,F为AB的中点
∴AB=DB,∠2=60°,∠DFB=90°
在直角△ABC中,
∠1=90°-30°=60°
∴∠DFB=∠ACB
∠2=∠1
DB=AB
∴△DFB≌△ACB
∴BF=BC
∵F为AB的中点
∴BF=AF
∴BC=AF
在等边三角形ACE中
AC=EA
∠EAC=60°
∴∠EAC+∠BAC=60°+30°=∠ACB
∴△ACB≌△EAF
∴△DFB≌△EAF————①成立
∴DF=AC
在等边△ACE中,AC=AE,∠3=60°
∴DF=AE————而在直角三角形ADF中,AD>DF,∴AD>AE,②错误
∵∠DFA=180°-∠DFB=90°,∠EAF=60°+30°=90°
∴∠DFA=∠EAF
∴DF//AE
∴四边形ADFE是平行四边形
∴AD//EF
∴∠AOE=∠DAC
而∠DAC=60°+30°=90°
∴∠AOE=90°
∴EF⊥AC————③成立
∵四边形ADFE是平行四边形
∴AG=GF=![]() AF
AF
∴AG=![]() AB
AB
∵AB=AD
∴AG=![]() AD
AD
即AD=4AG————④成立
知识点:作等边三角形
略
略








