如图，P是等边三角形ABC内一点，PE∥AB交BC于E，PF∥BC交AC于F，PG∥AC交AB于G，你能得出PE，PF，PG的和与△ABC的边长的关系吗？说明你的理由．
答案
解：PE+PF+PG=BC
理由：分别延长GP、FP交BC、AB于N、M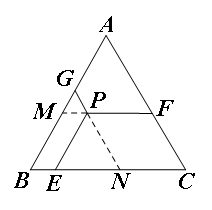
由题意：PE∥AB、MF∥BC、NG∥AC
∴四边形MPEB和四边形NPFC均为平行四边形
且
=60°，
=60°，
=60°
∴△GPM与△EPN均为等边三角形
∴PG=PM=BE，PF=NC，PE=EN
∴PE+PF+PG=EN+NC+BE=BC
知识点：线段间的关系
略
略
WORD格式（
