如图已知△ABC，AD是BC边上的中线，分别以AB边、AC边为直角边各向形外作等腰直角三角形，求证EF＝2AD.

答案

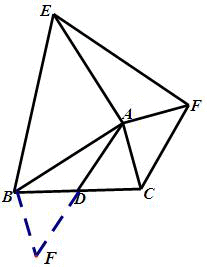
延长AD于H使AD=HD，连接BH。在三角形BDH与三角形CDA中
     BD=DC
      $\angle$ BDH= $\angle$ CDA
      DH=DA
$\therefore$ 三角形BDH $\stackrel{\backsim}{=}$ 三角形CDA（SAS）
$\therefore$ AC=BH， $\angle$ H= $\angle$ CAD。
$\therefore$ AC//BH， $\angle$ CAB+ $\angle$ ABF=180⁰.
$\because$    $\angle$ EAB+ $\angle$ CAF=90⁰+90⁰=180⁰.
$\therefore$ $\angle$ CAB+ $\angle$ EAF=180⁰
$\therefore$ $\angle$ ABH= $\angle$ EAF
在三角形EAF与三角形ABH中
      EA=BA
      $\angle$ EAF= $\angle$ ABH
      AF=AC=BH
$\therefore$ 三角形EAF $\stackrel{\backsim}{=}$ 三角形ABH（SAS）
$\therefore$ EF=AH=2AD。

知识点：全等三角形的判定与性质直角三角形的性质等腰直角三角形

见答案

不能正确的做出辅助线，实现变量之间的转化。

下载次数：2

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>