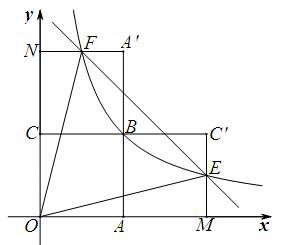
如图，四边形OABC是面积为4的正方形，函数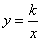
(x> 0)的图象经过点B.
（1）求k的值；
（2）将正方形OABC分别沿直线AB，BC翻折，得到正方形MABC′，NA'BC.设MC′、NA′分别与函数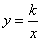(x>0)的图象交于点E、F，求线段EF所在直线的解析式．
（3）求△OEF的面积．
答案
解：（1）∵四边形OABC是面积为4的正方形
∴BC=BA=2，点B（2，2）在函数
的图象上
∴k=2×2=4
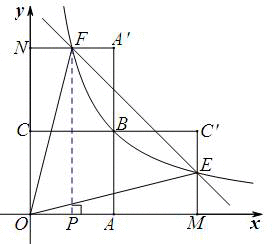
（2）依题意可知，N点坐标为（0，4），M点坐标为（4，0）
则点E、F的坐标分别为（4，1）和（1，4）
采用待定系数法可得E、F所在直线的表达式为
（3）过点F作FP⊥x轴于点P，由（2）可知FP=4，MP=3，ME=1
由反比例函数k的几何意义可知
知识点：反比例函数、四边形
略
略
WORD格式（
