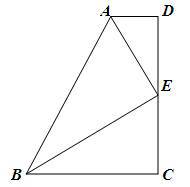
如图，四边形ABCD中，AD∥BC，AB=AD+BC，E是CD的中点。
求证：AE⊥BE．

答案

证明：延长AE交BC的延长线与点F，

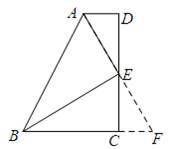
∵AD∥BC
∴∠D=∠DCF，∠DAE=∠F
∵E是CD的中点
∴DE=CE
在△ADE和△FCE中，

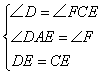
∴△ADE≌△FCE（AAS）
∴AD=FC，AE=FE
∵AB=AD+BC
∴AB=CF+BC=BF
在△ABE和△FBE中，

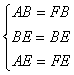
∴△ABE≌△FBE（SSS）
∴∠ABE=∠FBE=90°
即AE⊥BE

知识点：三角形全等之倍长中线  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>