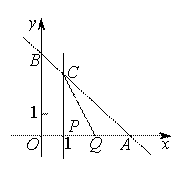
已知直线y=kx+3（k＜0）分别交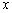
轴、
轴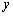于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作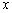轴的垂线交直线AB于点C，设运动时间为
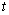秒．当k=-1时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时，两点同时停止运动．（1）直接写出当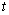＝1秒时，C、Q两点的坐标；（2）若以Q、C、A为顶点的三角形与△AOB相似，求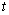的值．
轴、
轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作
秒．当k=-1时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时，两点同时停止运动．（1）直接写出当
答案
（1）C（1，2），Q（2，0）
（2）由题意得：P（t，0），C（t，﹣t+3），Q（3﹣t，0）
分两种情况讨论：
情形一：当△AQC∽△AOB时，∠AQC=∠AOB=90°，
∴CQ⊥OA，
∵CP⊥OA，
∴点P与点Q重合，
OQ=OP，
即3﹣t=t，
∴t=1.5
情形二：当△ACQ∽△AOB时，∠ACQ=∠AOB=90°，
∵OA=OB=3
∴△AOB是等腰直角三角形
∴△ACQ也是等腰直角三角形
∵CP⊥OA
∴AQ=2CP，即t=2（﹣t+3）
∴t=2
∴满足条件的t的值是1.5秒或2秒．
知识点：动点中的相似问题
由s=vt，将线段长度用含t的表达式表示出来，然后根据几何特征建立等式即可求解
略
WORD格式（
