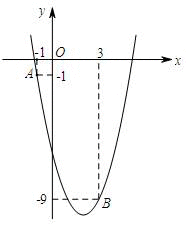如图，已知二次函数y=ax²-4x+c的图象经过点A和点B.
（1）求该二次函数的表达式；
（2）直接写出该抛物线的对称轴及顶点坐标；
（3）点P（m，m）与点Q均在该函数图象上（其中m＞0），且这两点关于抛物线的对称轴对称，求m的值及点Q到x轴的距离.

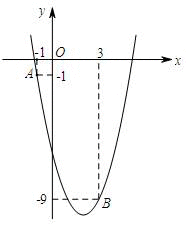
答案

（1）将x=-1，y=-1；x=3，y=-9，分别代入y=ax²-4x+c
得
解得
∴二次函数的表达式为y=x²-4x-6.
（2）对称轴为x=2；顶点坐标为（2，-10）.
（3）将（m，m）代入y=x²-4x-6，
得m=m²-4m-6，
解得m₁=6，m₂=-1（舍去）
.∴m=6，
∵点P与点Q关于对称轴x=2对称，
∴点Q到x轴的距离为6.

知识点：二次函数综合题  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>