如图,在△ABC中,∠1=∠2,点G为AD中点,延长BG交AC于点E,F为AB上一点,且CF⊥AD于点H,下列判断中:①线段BG是△ABD边AD上的中线;②线段CH是△ACH中AH边上的高;③△ABG与△BDG面积相等;④∠2+∠FBC+∠FCB=90°.其中正确的结论有( )
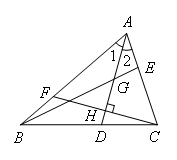
- A.4个
- B.3个
- C.2个
- D.1个
答案
正确答案:A
①因为G为AD中点,
所以BG是△ABD边AD上的中线,正确;
②因为CF⊥AD于点H,
所以CH是△ACH中AH边上的高,正确;
③因为G为AD中点,
所以AG=AD,
所以等底等高的三角形面积相等,正确;
④因为∠1=∠2,CF⊥AD,
所以∠AFH=90°-∠1=90°-∠2,
所以∠BFC=180°-∠AFH=90°+∠2,
因为∠BFC+∠FBC+∠FCB=180°,
所以90°+∠2+∠FBC+∠FCB=180°,
所以∠2+∠FBC+∠FCB=90°,正确.
所以正确的个数是4个.
故选:A.
略





