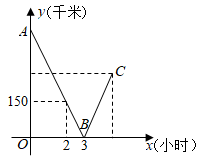
一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲、乙两地的距离为450千米;②轿车的速度为70千米/小时;
③货车的速度为60千米/小时;
④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
- A.1
- B.2
- C.3
- D.4
答案
正确答案:C
知识点:一次函数的应用
由图象可得,
甲、乙两地的距离为:150×3=450(千米),故①正确;
因为两车相遇时轿车比货车多行驶了90千米,
所以轿车每小时比货车多行驶90÷3=30(千米),
所以轿车的速度为:(450÷3+30)÷2=90(千米/小时),故②错误;
货车的速度为:(450÷3-30)÷2=60(千米/小时),故③正确;
点C的实际意义是轿车出发450÷90=5小时后到达乙地,
此时两车间的距离为:(90+60)×(5-3)=300(千米),故④正确;
故选:C.
略





