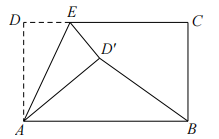
如图,长方形ABCD中,AD=BC=3,AB=CD=5,点E为射线DC上的一个动点,将△ADE沿AE折叠得到△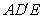 ,连接
,连接 ,当△
,当△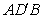 为直角三角形时,DE的长为( )
为直角三角形时,DE的长为( )
- A.1或4
- B.
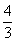 或9
或9 - C.1或9
- D.
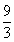 或1
或1
答案
正确答案:C
知识点:勾股定理之折叠问题
①如图,当∠![]() =90°时,
=90°时,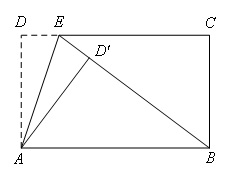
因为∠![]() =∠D=∠
=∠D=∠![]() =90°,
=90°,
所以B,![]() ,E三点共线,
,E三点共线,
因为![]() ,
,
所以BE=AB=5,
因为![]() =4,
=4,
所以![]() ;
;
②如图,当![]() =90°时,
=90°时,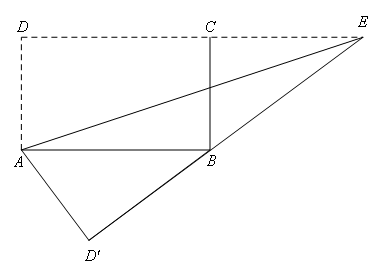
因为![]() =∠BCE=90°,
=∠BCE=90°,![]() =AD=BC=3,AB=CD=5,
=AD=BC=3,AB=CD=5,
所以由勾股定理得:![]() =4,
=4,
设CE=x,则![]() =DE=x+5,
=DE=x+5,
所以BE=![]() -
-![]() =x+1,
=x+1,
因为![]() ,
,
所以![]() ,
,
解得:x=4,
所以DE=CD+DE=5+4=9,
综上,DE的值为1或9,
故选:C.
略





