在△ABC中，AC=BC，∠ACB=90°，点M是AC上的一点，点N是BC上的一点，沿着直线MN折叠，使得点C恰好落在边AB上的P点．求证：MC：NC=AP：PB．
答案
证明：方法一：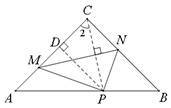
连接PC，过点P作PD⊥AC于D，则PD//BC
根据折叠可知MN⊥CP
∵∠2+∠PCN=90°，∠PCN+∠CNM=90°
∴∠2=∠CNM
∵∠CDP=∠NCM=90°
∴△PDC∽MCN
∴MC：CN=PD：DC
∵PD=DA
∴MC：CN=DA：DC
∵PD//BC
∴DA：DC=PA：PB
∴MC：CN=PA：PB
方法二：如图，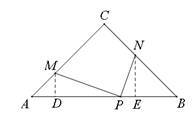
过M作MD⊥AB于D，过N作NE⊥AB于E
由双垂直模型，可以推知△PMD∽NPE，则
，
根据等比性质可知
，而MD=DA，NE=EB，PM=CM，PN=CN，
∴MC：CN=PA：PB
知识点：构造相似辅助线——双垂直模型
略
略
WORD格式（
