如图1，在四边形ABCD中，AB=AD，∠ABC+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=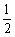∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系．
（1）思路梳理
将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合，由∠ABC+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线，易证△AFG≌       ，故EF，BE，DF之间的数量关系为               ．
（2）类比引申
如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC的延长线上，试猜想EF，BE，DF之间的数量关系，并给出证明．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°，若BD=1，EC=2，则DE的长为         ．

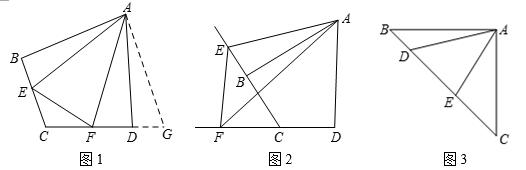
答案

（1）△AFE，EF=BE+DF；
（2）EF=DF-BE；
（3）．

知识点：全等三角形的判定与性质  旋转变换问题  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>