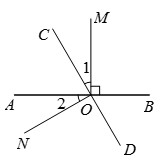
如图，直线AB，CD相交于点O，OM⊥AB于点O．
（1）若∠1=∠2，则ON与CD垂直吗？为什么？
（2）若∠BOC=4∠1，求∠AOC的度数．

解：（1）因为OM⊥AB于点O，
所以∠AOM＝∠BOM＝90°，
所以∠1+∠AOC＝90°，
因为∠2＝∠1，
所以∠2+∠AOC＝90°，
所以∠NOC＝90°；
（2）因为OM⊥AB于点O，
所以∠AOM＝∠BOM＝90°，
因为∠BOC＝4∠1，
所以∠BOM＝∠BOC﹣∠1＝4∠1﹣∠1＝90°，
所以∠1＝30°，
所以∠AOC＝∠AOM﹣∠1＝90°﹣30°＝60°．

略