如图，在△ABC中，AB=AC，AB＞BC，点D在边BC上，点E，F在线段AD上，且DF=2AF，∠1=∠2=∠BAC．若BE的长为5，求AD的长．

解：∵∠1=∠BAC，∠1=∠EBA+∠BAE，∠BAC=∠FAC+∠BAE，
∴∠EBA=∠FAC，
又∵∠1=∠2
∴180°-∠1=180°-∠2，
∴∠AEB=∠CFA，
在△ABE和△CAF中，，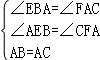
∴△ABE≌△CAF（AAS）
∴BE=AF=5，
∴DF=2AF=10，
∴AD=AF+DF=5+10=15

略