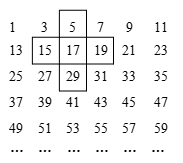
将连续奇数1，3，5，7，…排成如下的数表，十字框中框出5个数．
（1）十字框中框出的5个数的和与框子中间的数17有什么关系？
（2）若设中间的数为a，则代数式表示十字框中框出的5个数字之和．
（3）十字框中框出的5个数之和能等于2 020吗？能等于2 055吗？若不能，说明理由；若能，求出这5个数，并指出这5个数中的中间数位于第几行的第几个数．

（1）因为5+15+17+19+29=85=17×5，
所以十字框框住的5个数的和是17的5倍；
（2）若设中间的数为a，则上面的为a-12，下面的为a+12，左面的为a-2，右面的为a+2，
所以a+（a-2）+（a+2）+（a-12）+（a+12）=5a；
（3）当5a=2020时，得a=404，
因为a不是奇数，
所以5个数之和不能等于2020．
当5a=2055时，a=411
因为a是奇数
所以，5个数之和可以是2055
这五个数是399，409，411，413，423，中间数是位于第68行第4个数
，所以411是第206个奇数，一行是6个数，206÷6=34……2，所以a是位于第35行第2个数

略