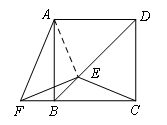
（2021包头）如图，BD是正方形ABCD的一条对角线，E是BD上一点，F是CB延长线上一点，连接CE，EF，AF．若DE=DC，EF=EC，则∠BAF的度数为____．

解：如图，连接AE，

∵BD为正方形ABCD的对角线，
∴∠BDC=45°，
∵DE=DC=AD，
∴∠DEC=∠DCE==67.5°，
∵∠DCB=90°，
∴∠BCE=90°-∠DCE=90°-67.5°=22.5°，
∵EF=EC，
∴∠FEC=180°-∠EFC-∠ECF=180°-22.5°-22.5°=135°，
∵∠BEC=180°-∠DEC=180°-67.5°=112.5°，
∴∠BEF=135°-112.5°=22.5°，
∵AD=DE，∠ADE=45°，
∴∠AED==67.5°，
∴∠BEF+∠AED=22.5°+67.5°=90°，
∴∠AEF=180°-90°=90°，
在△ADE和△EDC中，

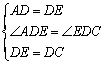
∴△ADE≌△EDC（SAS），
∴AE=EC，
∴AE=EF，
即△AEF为等腰直角三角形，
∴∠AFE=45°，
∴∠AFB=∠AFE+∠BFE=45°+22.5°=67.5°，
∵∠ABF=90°，
∴∠BAF=90°-∠AFB=90°-67.5°=22.5°．

略