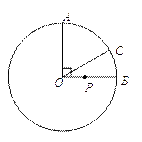
如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值为().
- A.2
- B.

- C.
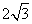
- D.
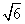
答案
正确答案:C
知识点:轴对称-最短路线问题
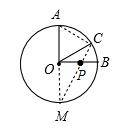
作A关于OB的对称点M,连接MC,交OB于P,PA+PC的最小值即为MC的长。由∠AOC=60°,可得△AOC是等边三角形,所以AC=2;因为AM为直径,所以∠ACM=90°,在Rt△AMC中,由勾股定理得MC=![]()
略




正确答案:C
知识点:轴对称-最短路线问题
作A关于OB的对称点M,连接MC,交OB于P,PA+PC的最小值即为MC的长。由∠AOC=60°,可得△AOC是等边三角形,所以AC=2;因为AM为直径,所以∠ACM=90°,在Rt△AMC中,由勾股定理得MC=![]()

略
