二次函数y＝－＋6的图象与x轴从左到右两个交点依次为A、B，与y轴交于点C．
（1）求A、B、C三点的坐标；
（2）如果P(x，y)是抛物线AC之间的动点，O为坐标原点，试求△POA的面积S与x之间的函数关系式，并写出自变量x的取值范围；
（3）是否存在这样的点P，使得PO=PA，若存在求出点P的坐标；若不存在说明理由．

如图：

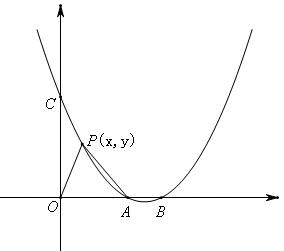
（1）抛物线的解析式中，令x=0可得C点坐标，令y=0，可得A、B的坐标；因此，A（4，0），B（6，0），C（0，6）；
（2）△POA的面积就等于底边OA的长乘以点P的纵坐标的积的一半，因此，S＝OA×y×，因P点是在抛物线上的，所以y＝－＋6，并且OA＝4，所以S＝－5x＋12.（0≤x≤4）
（3）若存在这样的点满足PO＝PA，则△POA就是等腰三角形，所以点P即在OA的垂直平分线上，即点P的横坐标为x＝2，代入抛物线的方程可得，y＝2，所以点P的坐标为（2，2）.

对于题中的第（3）问不能很好的将代数的关系转化为几何的关系