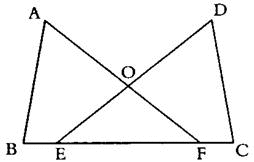
已知：如图，B、E、F、C四点在同一条直线上，AB＝DC，BE＝CF，∠B＝∠C.求证：OA＝OD.
答案
∵BE=CF
∴BE+EF=CF+FE，BF=CE
∵BF=CE
∠B＝∠C.
AB＝DC
∴△ABF≌ △DCE（SAS）
∴AF=DE，∠AFB=∠DEC
∵∠AFB=∠DEC
∴△EOF为等腰三角形，OE=OF
∴AF-OF=DE-OE
∴AO=DO
知识点：全等三角形的判定与性质 等腰三角形的性质
要证明OA＝OD，题目中并没有给足证明包含OA和OD的三角形全等的条件。分析已知条件AB＝DC，BE＝CF，∠B＝∠C，通过变换可以得到BE+EF=CF+FE，即BF=CE，
利用SAS证明出△ABF≌ △DCE，
∴∠AFB=∠DEC，AF=DE。
∵∠AFB=∠DEC，∴△EOF为等腰三角形，即OE=OF，
∴AF-OF=BE-OE，即OA=OD，得证。
转化思想
WORD格式（
