已知：如图，直线AB∥CD，且OD与AC相交于点O．若∠BAC=140°，∠ODC=30°，求∠COD的度数．

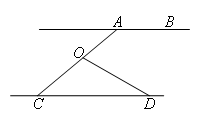
解：如图，

在△OCD中，∠ACD+∠ODC+∠COD=180°（三角形内角和定理）
∵∠ACD=40°（已证），∠ODC=30°（已知）
∴∠COD=180°-∠ACD-∠ODC
=180°-40°-30°
=110°（等式的性质）
横线处应填写的过程最恰当的是( )

A.∵AB∥CD（已知）∴∠BAC+∠ACD=180°（两直线平行，同旁内角互补）∵∠BAC=140°（已知）∴∠ACD=180°-∠BAC=180°-140°=40°（等式的性质）
B.∵∠BAC+∠ACD=180°（两直线平行，同旁内角互补）∠BAC=140°（已知）∴∠ACD=180°-∠BAC=180°-140°=40°（等式的性质）
C.∵∠BAC=140°（已知）∴∠ACD=180°-∠BAC=180°-140°=40°（两直线平行，同旁内角互补）
D.∵AB∥CD（已知）∴∠ACD=180°-∠BAC=180°-140°=40°（两直线平行，同旁内角互补）

答案

正确答案：A

知识点：略

略

下载次数：0