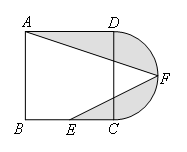
如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是(    )

分析：求不规则图形面积考虑利用割补法转化为求规则图形的面积．连接AE，把空白图形分为两个三角形，阴影部分面积就等于正方形ABCD加上半圆的面积，减去两个三角形的面积．
解答：如图，连接AE，过点F作FG⊥BC交BC延长线于点G，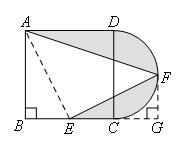

则，
∵以CD为直径作半圆CFD，点F为半圆的中点
∴CG=FG=6，
∵点E为BC的中点，
∴BE=CE=6，
∴EG=CE+CG=12，
∴BE=FG，AB=EG，
∴△ABE≌△EGF（SAS），
∴AE=EF，，
∵，
∴，
∴，
∴△AEF为等腰直角三角形，
在Rt△ABE中，由勾股定理得．
∴

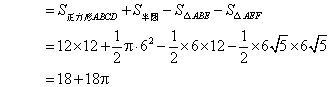
略