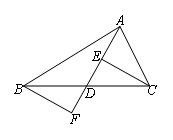
如图，AD是△ABC的中线，点E在AD上，点F在AD的延长线上，且DE=DF，连接BF，CE，求证：BF∥CE．

证明：如图，
∵AD是△ABC的中线
∴BD=CD
在△BDF和△CDE中
                           
∴BF∥CE
以上空缺处所填错误的是(    )

• A.
• B.
• C.
• D.

答案

正确答案：B

知识点：全等三角形的性质  全等三角形的判定  

证明：如图，

∵AD是△ABC的中线
∴BD=CD
在△BDF和△CDE中

∴△BDF≌△CDE(SAS)
∴∠F=∠DEC(或∠FBD=∠ECD)（全等三角形对应角相等）
∴BF∥CE
B选项中把未知的条件(∠F=∠DEC)当成已知来用，因此不正确，
故选B．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题