如图,在△ABC中,∠ACD=90°,AC=BC,AE⊥BF于点E,交BC于点D;
求证:△ADC≌△BFC
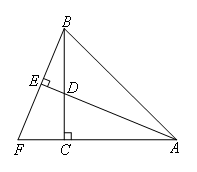
证明:如图,
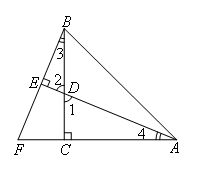
∵AE⊥BF
∴∠BED=90°
∴∠3+∠2=90°
∵∠ACD=90°
∴∠1+∠4=90°
∵∠1=∠2
∴∠3=∠4
∵∠ACD=90°
∴∠BCF=90°
∴∠ACD=∠BCF
在△ADC和△BFC中
∴
①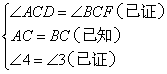 ;②
;②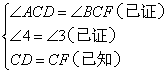 ;
;
③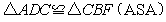 ;④
;④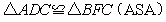 .
.
以上空缺处依次所填最恰当的是( )
- A.①③
- B.②③
- C.①④
- D.②④
答案
正确答案:C
知识点:全等三角形的判定
1.解题思路
要证△ADC≌△BFC,需要找三组条件,
题中给出了一组对应边AC=BC,因此还需要找两组条件.
根据题中给出的垂直和90°进行导角,
可以得到∠ACD=∠BCF,∠CAD=∠CBF这两组对应角,
因此用ASA证明三角形全等.
2.解题过程
证明:如图,
∵AE⊥BF
∴∠BED=90°
∴∠3+∠2=90°
∵∠ACD=90°
∴∠1+∠4=90°
∵∠1=∠2
∴∠3=∠4
∵∠ACD=90°
∴∠BCF=90°
∴∠ACD=∠BCF
在△ADC和△BFC中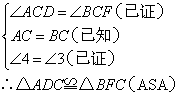
因此,空缺处依次填写最恰当的是①④,
故选C.
略








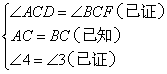 ;②
;②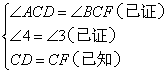 ;
;