已知:如图,AB∥FC,DE=FE,AB=15,CF=8,求BD的长.
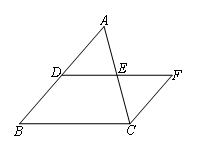
解:如图,
∵AB∥FC
∴∠ADE=∠F
在△ADE和△CFE中
∴△ADE≌△CFE(ASA)
① ;②
;② ;
;
③ ;④
;④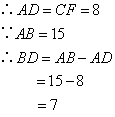 ;
;
⑤ .
.
以上空缺处依次所填最恰当的是( )
- A.①④
- B.①⑤
- C.②③
- D.②⑤
答案
正确答案:D
知识点:全等三角形的判定与性质
1.解题思路
根据AB∥FC,DE=FE可以证明△ADE≌△CFE,
由全等三角形对应边相等得AD=CF,进而就可求得BD的值.
2.解题过程
解:如图,
∵AB∥FC
∴∠ADE=∠F
在△ADE和△CFE中
∴△ADE≌△CFE(ASA)
∴AD=CF(全等三角形对应边相等)
∵CF=8
∴AD=8
∵AB=15
∴BD=AB-AD
=15-8
=7
第1个空,①中的![]() ,题目中没有证明,不能直接用,
,题目中没有证明,不能直接用,
因此应填②;
第2个空,结合证明过程可知,应填⑤.
因此空缺处依次所填最恰当的是②⑤.
故选D.
略







 ;②
;② ;
; ;④
;④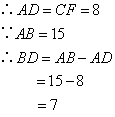 ;
; .
.