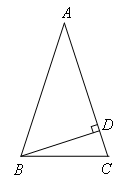
如图,在△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
- A.36°
- B.24°
- C.30°
- D.18°
答案
正确答案:D
知识点:略
分析:要求∠DBC的度数,可以把∠DBC放在Rt△DBC中,
求出∠C的度数就可以得出∠DBC的度数;
△ABC是等腰三角形,顶角的度数已知,
因此两底角的度数可以求出,即∠C的度数可以求出.
过程示范:
∵AB=AC
∴∠ABC=∠C
∵∠A=36°
∴∠ABC=∠C=![]()
∵BD是AC边上的高
∴BD⊥AC
∴∠BDC=90°
∴∠DBC=90°-∠C
=90°-72°
=18°
故选D.
略








