已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.若∠EOD=30°,则CE的长为( )

- A.2
- B.
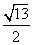
- C.
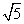
- D.
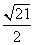
答案
正确答案:D
知识点:略
1.思路分析
根据菱形的对角线平分一组对角求出∠DAO=30°,证明
∠AEF=90°,即△CEF为直角三角形,再求出EF,CF的长.
在Rt△CEF中,利用勾股定理即可求解.
2.解题过程
在菱形ABCD中,∠BAD=60°,AB=2,
AO=CO,AD∥BC,∠DAO=30°,
∴∠OAE=∠OCF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,OE=OF,
∵∠EOD=30°,
∴∠AOE=60°,
∴∠AEF=90°,
∴∠CFE=90°,
∴OD=1,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在Rt△CEF中,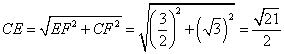 .
.
故选D
略








