如图,∠AOB=30°,点M,N分别在边OA,OB上,且OM=2,ON=6,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是( )

- A.
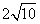
- B.
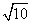
- C.20
- D.
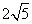
答案
正确答案:A
知识点:略
点M,N是定点,点P,Q是动点,且在定直线上运动,求线段的和最小,考虑作定点的对称点,分析转化、求解.
如图,作M关于OB的对称点M',作N关于OA的对称点N',求MP+PQ+QN的最小值就转化为求M'P+PQ+QN'的最小值,两点之间线段最短,最小值即为线段M'N'的长.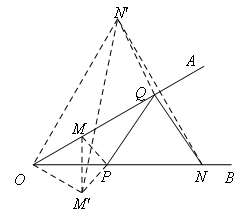
根据轴对称的性质,得
∠N'OA=∠M'OB=30°,OM'=OM=2,ON'=ON=6,
所以∠M'ON'=90°.
在Rt△M'ON'中,由勾股定理,得![]()
所以MP+PQ+QN的最小值为![]() .
.
故选A
略








