如图，四边形ABCD是边长为1的正方形，△BPC是等边三角形，连接DP并延长交CB的延长线于点H，连接BD交PC于点Q，下列结论：①∠BPD=135°；②△BDP∽△HDB；③DQ:BQ=1:2；④S_△BDP=．其中正确的有(    )

①∵四边形ABCD是正方形，△BPC是等边三角形，
∴∠BCP=60°，CP=CB=CD，
等腰三角形CPD中，∠CPD=，
∴∠BPD=60°+75°=135°，故正确．
②∵∠DBH=180°-∠DBC=180°-45°=135°，∠BDP=∠HDB，
∴∠BPD=∠DBH，
∴△BDP∽△HDB，故正确．
③如图，延长CP交AD于点M，

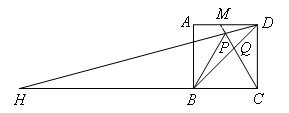
∵AD∥CB
∴DQ:BQ=DM:BC=DM:DC=1:，故错误．
④由②△BDP∽△HDB，
∴，若设BH=x，则HD=，
在Rt△HCD，HC²+CD²=DH²，即，
解得
由相似性质可得，
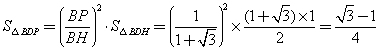，故正确．

略