如图,在正方形ABCD中,点E,F分别在BC,CD上,如果AE=3,EF=2,AF= ,则正方形的边长为( )
,则正方形的边长为( )

- A.
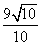
- B.
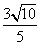
- C.
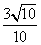
- D.
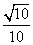
答案
正确答案:A
知识点:略
∵AE=3,EF=2,AF=![]() ,
,
由勾股定理逆定理可得,△AEF是直角三角形,且∠AEF=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠C=90°,
∴∠AEB+∠BAE=∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF,
∴![]() ,
,
设AB=3a,则EC=2a,
∴BE=BC-EC=AB-EC=a,
在Rt△ABE中,由勾股定理得AB2+BE2=AE2,
∴(3a)2+a2=32,
解得![]() ,
,![]() (舍),
(舍),
∴![]() .
.
略








